How Not to Get Your Sample Size

The video above walks through some common but poor sample-size planning practices: run-and-check (backing into a sample-size by chasing statistical significance) and uncritically adopting previous sample sizes.

In the explorations below you can dig into why run-and-check is so bad, and you can also explore the suprising fact that p < .05 does not mean you have an adequate sample size.

Exploration: Don’t Run-and-Check!

A common approach to sample-size determination is Run-and-Check: you run a small batch of samples, check for significance, and then keep adding samples until you either get what you want or run out of time/resources. Sometimes run-and-check is conducted over people/labs – keep assigning the same project to different trainees until someone with ‘good hands’ gets it to work (sometimes that really is good hands, but it can also easily be capitalization chance!).

Let’s examine why run-and-check is so dangerous to good science. We’ll simulate data for a two-group experiment, with the simulation set so that there is no true effect in the population. We’ll start with n = 3/group, then check. If the results are significant, we stop, otherwise we add 1 sample/group and check again, and so on, to a limit of n = 30 group. In this scenario, any statistically significant finding is a false positive. We’ll run 10,000 simulations and check the false-positive rate.

The code for the simulation is below. Before you scroll down to its output, what is your guess for the false positive rate for this run-and-check approach?

# If needed, install needed libraries
if (!require("statpsych")) install.packages("statpsych")
if (!require("ggplot2")) install.packages("ggplot2")
if (!require("gganimate")) install.packages("gganimate")
if (!require("gifski")) install.packages("gifski")


# Load needed libraries
library(statpsych)
library(ggplot2)
library(gganimate)


# Simulation parameters
n_initial <- 3
n_add_per_round <- 1
n_to_give_up <- 30
true_effect_size <- 0
total_sims <- 1000

# Initialize variables for results
false_positives <- 0
randc_res <- data.frame(p = NA, n = NA, sample = NA, eventually_significant = NA)
results_row <- 0

# simulation 
for (i in 1:total_sims) {
  
  # simulate data at initial sample size for both groups and do t.test
  n_current <- n_initial
  g1 <- rnorm(n_current, 0, 1)
  g2 <- rnorm(n_current, 0 + true_effect_size, 1)
  res <- t.test(g1, g2)$p.value
  results_row <- results_row + 1
  
  # store the results for plotting
  randc_res[results_row, ] <- c(
    res,
    n_current,
    i,
    FALSE
  )
  
  # if not significant and not at n_to_give_up yet, keep going
  while (res >= .05 & n_current < n_to_give_up) {
    g1 <- c(g1, rnorm(n_add_per_round, 0, 1))
    g2 <- c(g2, rnorm(n_add_per_round, 0 + true_effect_size, 1))
    n_current <- n_current + n_add_per_round
    results_row <- results_row + 1
    res <- t.test(g1, g2)$p.value
    
    randc_res[results_row, ] <- c(
      res,
      n_current,
      i,
      FALSE
    )
  }
  
  # If the final result is significnt, that's a false positive (assuming true_effect_size == 0)
  if (res < .05) {
    false_positives <- false_positives + 1
    randc_res[randc_res$sample == i, ]$eventually_significant <- TRUE
  }
  
}


print(
  paste(
    "Simulated", total_sims, 
    "two-group studies with a true mean difference of", true_effect_size,
    "where sample sizes started off with", n_initial, "/group",
    "and if not significant added", n_add_per_round, "/group and re-checked,",
    "up to significance or a max sample size of", n_to_give_up, "."
  )
)
print("Proportion of significant findings")
print(false_positives / total_sims)

Simulation Results: False-Positive Rate

The code simulated 1000 two-group studies with a true mean difference 0 where sample sizes started off with 3/group and if not significant added 1/group up to significance or a max sample size of 30.

Under this scenario, the proportion of false positives is: 24.6%.

This scenario is a bit extreme, but it makes it clear that run-and-check is not a good method for determining sample size.

Simulation Results: The Deceptive Dance of the p Value

To make this even more clear, we’re going to plot the p values as sample sizes are added, cycling through the first 10 simulations(Figure 1). What you’ll notice is that the p values “feel” like they are following trajectories, swining higher or lower. This can give the researcher using run-and-check the feeling that they’re on to something, and that they are justified adding more samples, or worse, adjusting their analyses to coax the p value below .05.

Code 
randc_res$animate_frame <- 1:nrow(randc_res)
randc_res$eventually_significant <- as.factor(randc_res$eventually_significant)
randc_res$sample_as_factor <- as.factor(randc_res$sample)

pdance_plot <- ggplot(data = randc_res[randc_res$sample < 5 , ], aes(x = n, y = p, group = sample, colour = eventually_significant))
pdance_plot <- pdance_plot + ylab("Obtained p value")
pdance_plot <- pdance_plot + xlab("Sample size")
pdance_plot <- pdance_plot + geom_point(size = 3)
pdance_plot <- pdance_plot + theme_classic() + theme(legend.position = "none")
pdance_plot <- pdance_plot + geom_hline(yintercept = 0.05, linetype = "dotted")
pdance_plot <- pdance_plot + scale_colour_manual(values = c("1" = "red", "0" = "dodgerblue1"))
pdance_plot <- pdance_plot + ylim(c(0, 1))
pdance_plot <- pdance_plot + xlim(c(n_initial, n_to_give_up))
pdance_plot <- pdance_plot + transition_reveal(animate_frame, keep_last = FALSE)
animate(pdance_plot, fps = 2, renderer = gifski_renderer("run_and_check.gif"))
Figure 1: Evolution of p values as samples are added but no true effect

Thus, it’s not just the instinsic false-positive rate of run-and-check that is dangerous but also the false impression it can give that might license analytic flexibility towards erroneous results. For more on the perils of run-and-check see (Anscombe 1954; Simmons, Nelson, and Simonsohn 2011).

Exploration: The Perils of Inadequate Samples, Even When p < .05

Despite calls for sample-size plans, many researchers seem to avoid sample-size planning or conduct pro forma plans to evade the requirement. Why? One reason seems to be the misconception that if your lab gets p < .05, then you have nothing to worry about. Here’s an editorial where this sentiment was very clearly expressed:

However, somehow, journals have taken to asking how our animal studies were powered − and here’s the point: If the results are statistically significant then, indeed, our study is appropriately powered. Sometimes, I’m not sure that the editors who insist on this information understand this.

(Mole 2017)

This attitude is seductive, but ultimately incorrect (Mole 2018). It’s important to think this through for yourself so you can understand why inadequate samples are so problematic.

Imagine you are measuring the effect of maternal separation on gene expression in the hippocampus. You’ll have two groups: Control and Separated. You’ll use qPCR to measure expression of egr1, a constituitvely-expressed gene that plays an important role in learning and memory.

Without a sample-size plan, you’d likely rely on the previous literature or lab practices to set a sample size. In qPCR experiments like this one, n = 6/group is pretty common, so that’s what you decide to go with.

Let’s suppose that in this case, your research hypothesis is absolutely correct: maternal separation does produce a large and robust increase in egr1 expression. We’ll set the effect size at 1 standard deviation (Cohen’s d = 1; see the section on effect sizes if you’re not sure what this means).

This sounds like an ideal situation: the researcher has a hypothesis that is actually correct! Let’s see, though, what happens when this true hypothesis is investigated with n = 6/group.

Simulation

In the simulation below, we randomly generate gene-expression data for the Control and Separated groups, drawing the data from distributions that are 1 standard deviation apart. With each draw we then run a t-test and check to see if it is statistically significant or not. Given that the researcher’s hypothesis is true, we might expect this experiment to always “work”, regularly producing p < .05. In fact, though, it does not.!

# If needed, install needed libraries
if (!require("statpsych")) install.packages("statpsych")
if (!require("ggplot2")) install.packages("ggplot2")
if (!require("gganimate")) install.packages("gganimate")
if (!require("gifski")) install.packages("gifski")


# Load needed libraries
library(statpsych)
library(ggplot2)
library(gganimate)


# Simulation parameters
effect_size_in_sds <- 1
samples_per_group <- 6
alpha <- 0.05
simcount <- 10000

# Initialize variables for results
sigfindings <- 0
all_res <- data.frame(d = NA, p = NA, distortion = NA, sample = NA, CIlength = NA)

# Now do the simulations
for (i in 1:simcount) {
  # Control group 
  control <- rnorm(samples_per_group, 0, 1)
  # Experimental group
  experimental <- rnorm(samples_per_group, 0, 1) + effect_size_in_sds
  # Analyze with a t-test
  myres <- t.test(control, experimental)
  # Increase counter if a significant finding
  if (myres$p.value < alpha) sigfindings <- sigfindings + 1
  # Express this finding in Cohen's d
  myd <- statpsych::ci.stdmean2(
    alpha = alpha,
    m2 = mean(control),
    m1 = mean(experimental),
    sd2 = sd(control),
    sd1 = sd(experimental),
    n2 = length(control),
    n1 = length(experimental)
  )
  
  # Store the result of this sample
  all_res[i, ] <- c(
    myd[1, 2],
    myres$p.value,
    myd[1, 2] / effect_size_in_sds,
    i,
    myd[1, 5] - myd[1, 4]
  )
  
}

print(paste("Simulated", simcount, "2-group experiments with n =", samples_per_group, "/group and a true effect of", effect_size_in_sds, "standard deviations."))
print("Proportion of statistically significant findings (p < .05):")
print(sigfindings/simcount)
print("Typical margin of error:")
print(mean(all_res$CIlength/2))

Simulation Results: Power

The code above simulates 10000 2-group experiments with n = 6 and a true effect of 1 standard deviations.

Under this scenario, where there is a large effect, only 33.6% of samples yield statistically significant results (p < .05).

This sample-size is inadequate because the typical margin of error is 1.37

As you can see, only about 33% of experiments yield p < .05 even though there is a real and substantial effect to be observed! Why so low? Well, consider that statistical tests examine if the difference observed (signal) is substantially greater than expected sampling error (noise). With the sample-size we selected, though, expected sampling error is large: in fact, the margin of error in these studies is typically ~1.37 standard deviations, far larger than the signal it would be reasonable to expect!

If the noise in this type of study is bigger than the signal, how do any of the experiments still turn out to be statistically significant? This occurs when sampling error breaks in just the right way to distort the effect–to make it seem much bigger than it really is, so that, for that misleading sample at least, the effect observed is substantially larger than the real truth. Uh oh! That’s right, in these cases p < .05 can only occur by mis-characterizing the actual truth.

Simulation Results: Observed Effect Sizes

Let’s see this in more detail. Figure 2 plots the effect observed in each study. The line at 1 standard deviation represents the true effect. Because of sampling error, studies “dance” around this truth – some get a bit too large of an effect, others a bit too small. Notice, though, the coloring, which represents statistical significance of each simulated experiment. Most of the dots are blue, not significant – that’s the low power of the experiment. But note that the statistically significant findings (the red dots) all studies that radically over-estimated the real truth:

Code 
time_plot <- ggplot(data = all_res[all_res$sample < 200, ], aes(x=sample, y = d, colour = (p < alpha)))
time_plot <- time_plot + ylab("Standardized Mean Difference in egr Expression (Experimental vs. Control)")
time_plot <- time_plot + geom_point(aes(group = sample))
time_plot <- time_plot + theme_classic() + theme(legend.position = "none")
time_plot <- time_plot + scale_colour_manual(values = c("TRUE" = "red", "FALSE" = "dodgerblue1"))
time_plot <- time_plot + geom_hline(yintercept = 0, linetype = "dotted")
time_plot <- time_plot + geom_hline(yintercept = 1)
time_plot <- time_plot + transition_reveal(sample)
animate(time_plot, fps = 6, renderer = gifski_renderer("d_over_time_updated.gif"))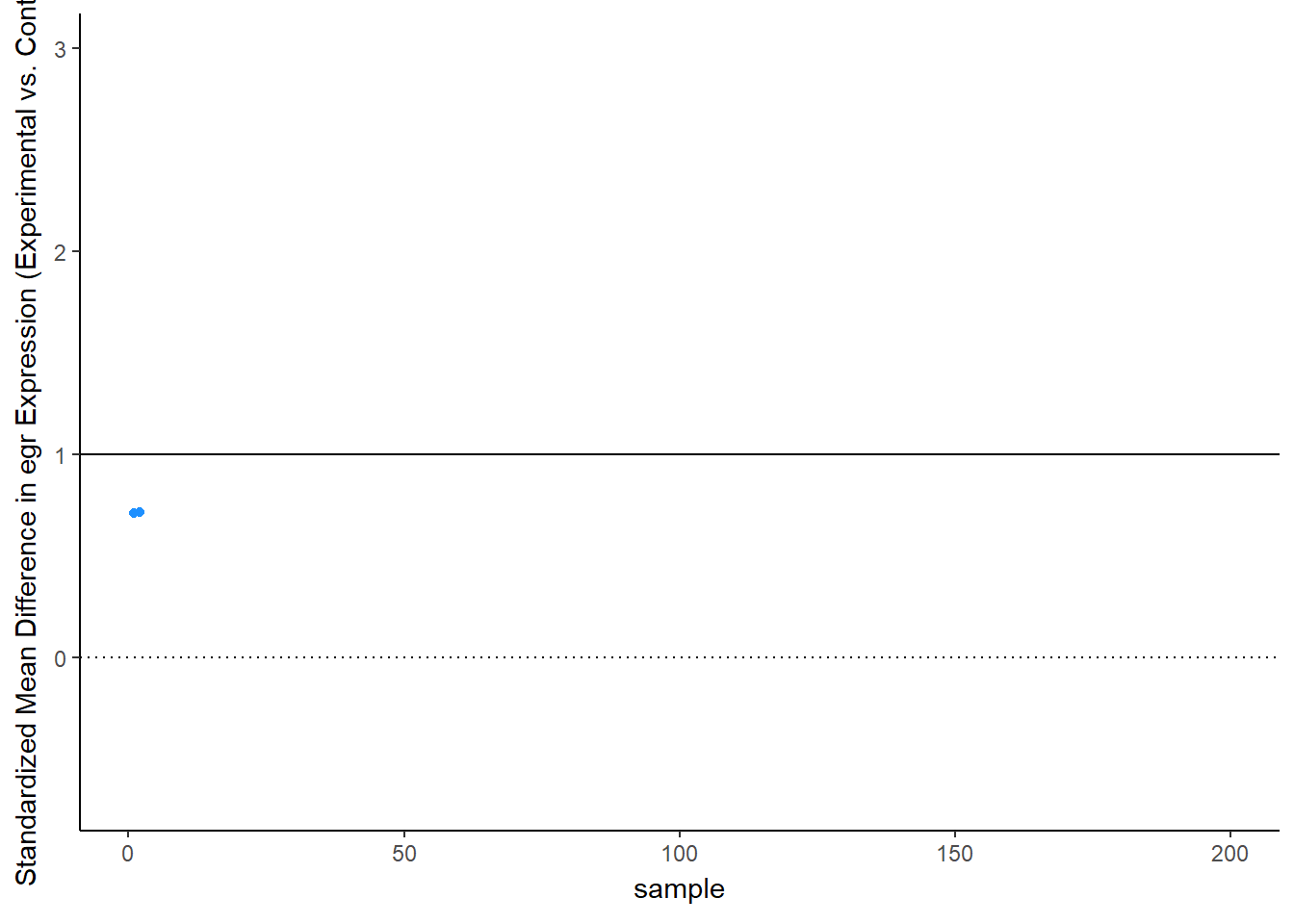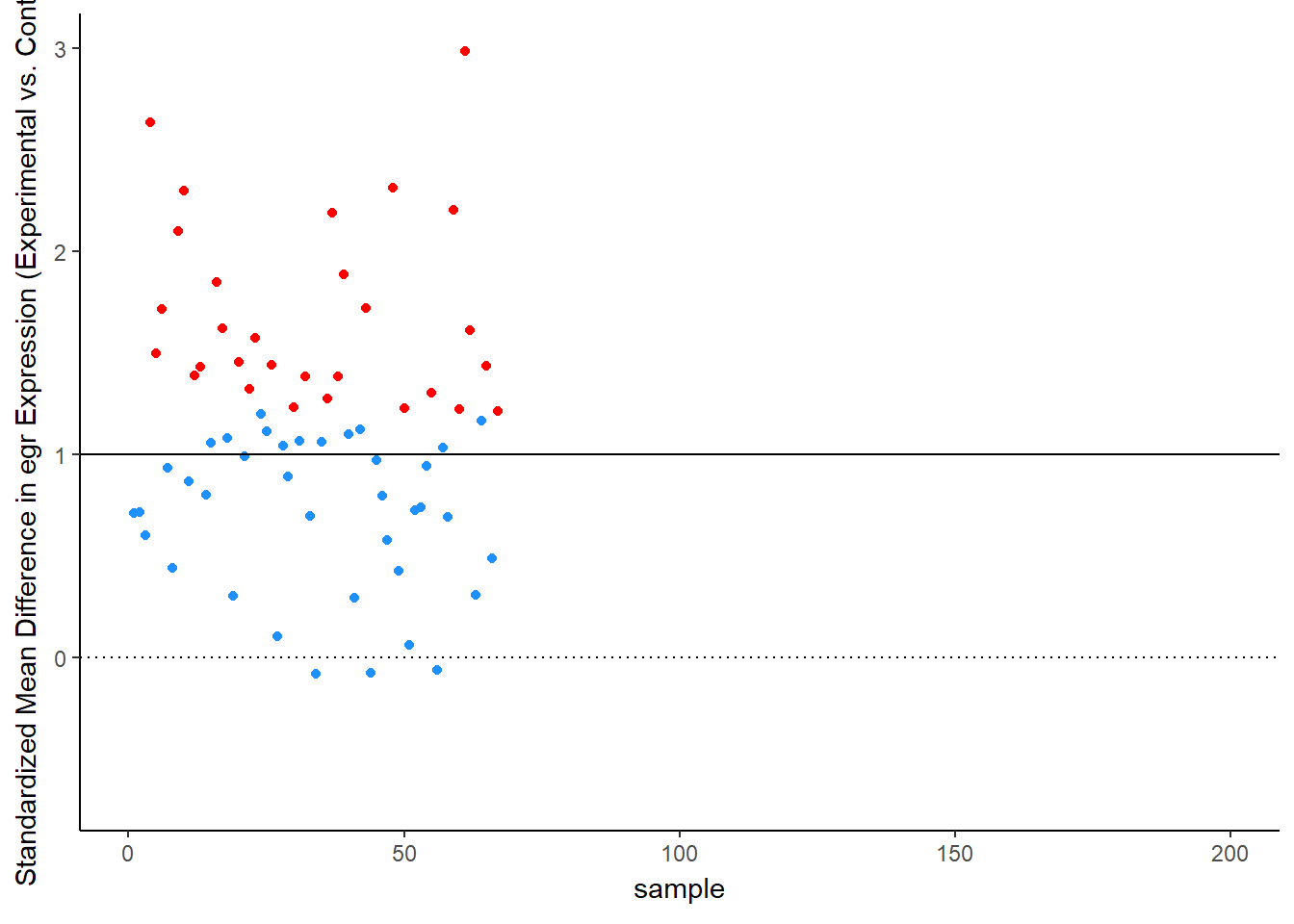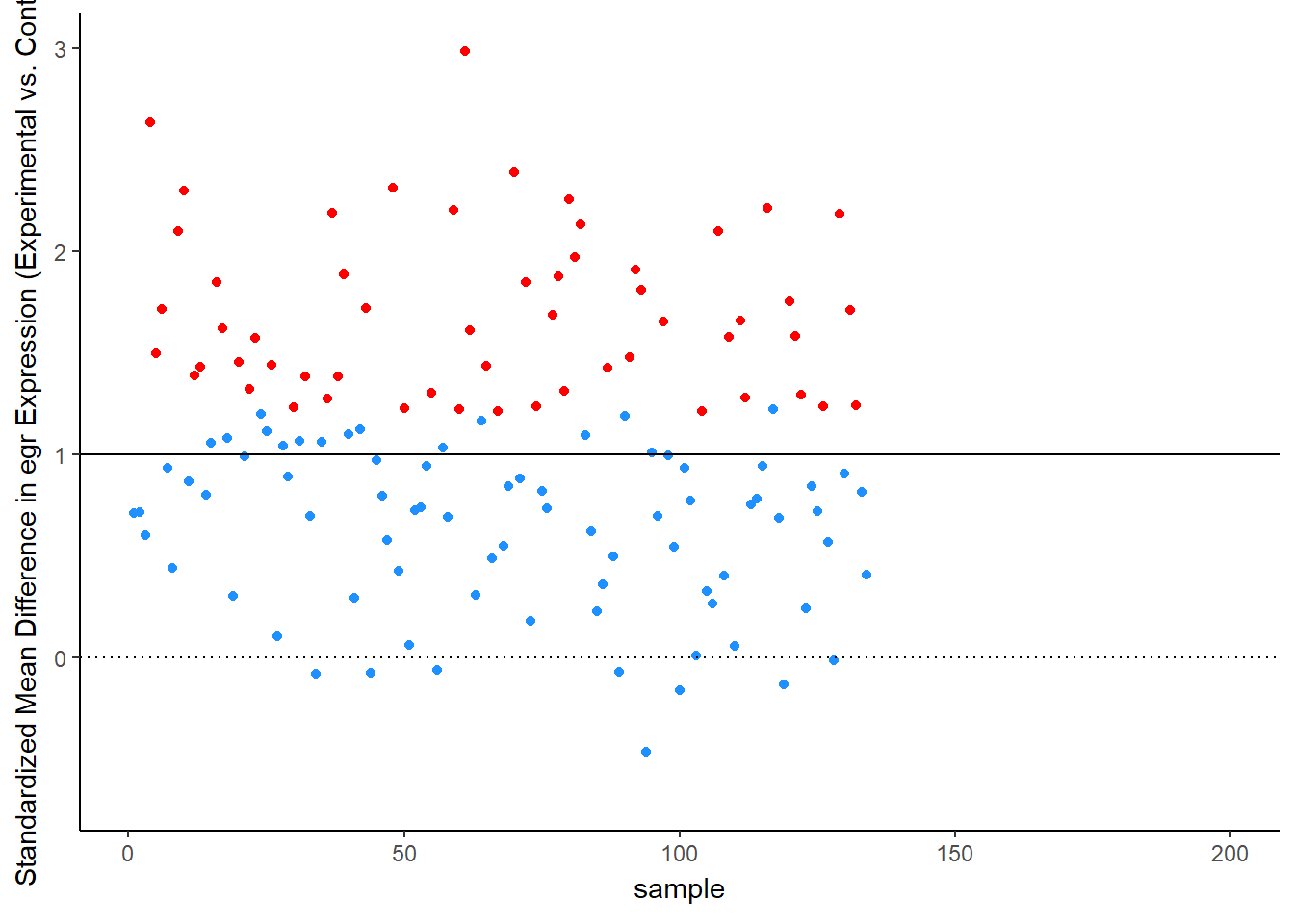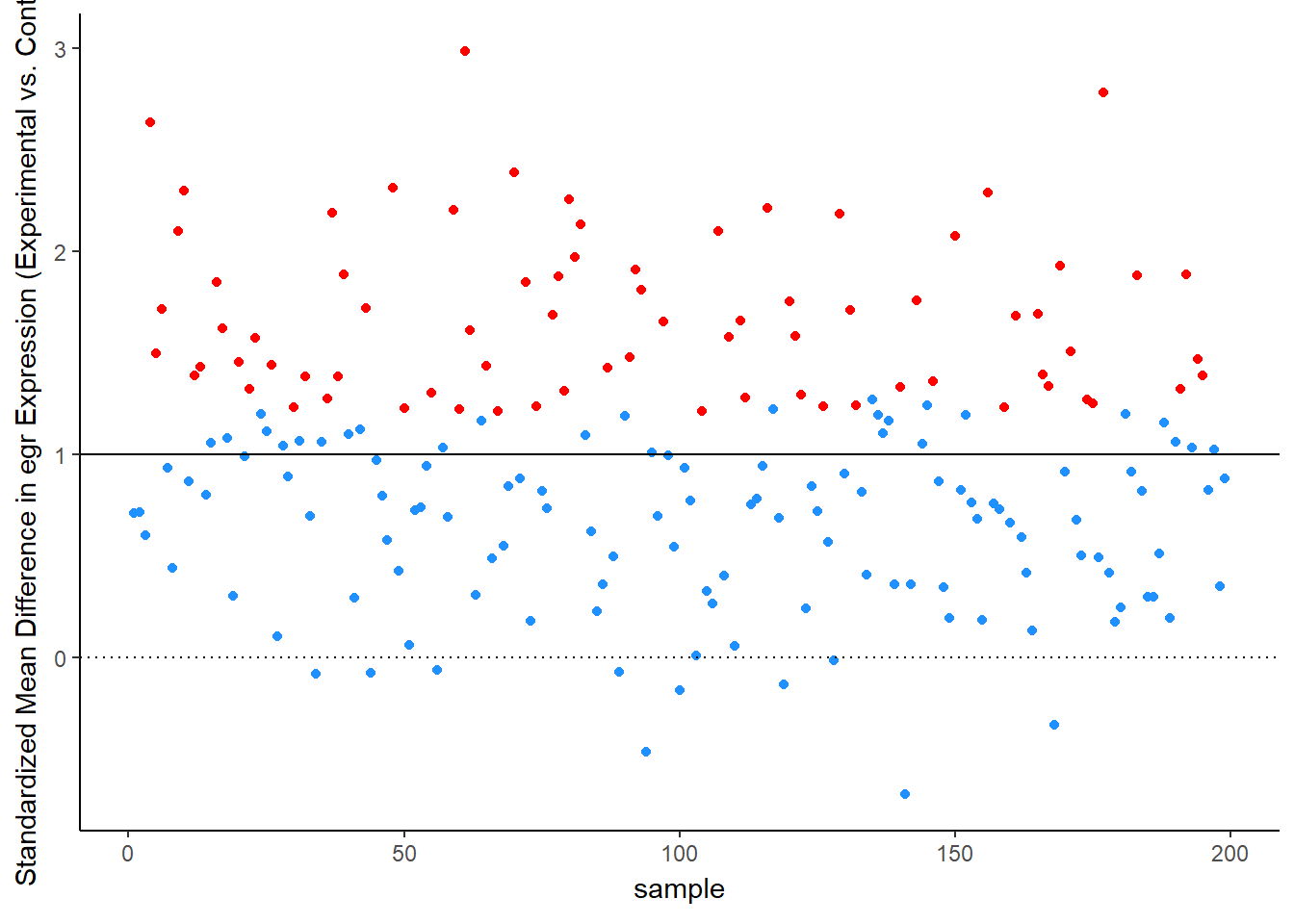
Figure 2: Observed effect sizes by stat significance status.

Simulation Results: Effect-Size Inflation Among Significant Results

How bad is this over-estimation? Let’s find out:

print("In this scenario, the true effect size is 1 standard deviations")
print("Across all stimulated studies, the average effect size observed is:")
mean(all_res$d)
print("But for the studies that reached statistical significance, the average effect size observed is:")
mean(all_res[all_res$p < .05, ]$d)

  • In this scenario, the true effect size is: 1 standard deviations

  • Across all stimulated studies, the average effect size observed is: 1.00

  • But for the studies that reached statistical significance, the average effect size observed is: 1.70

Wow! The statistically-significant effects over-state the truth by over 70%. Below is a representation of the true effect and the effect that would be reported through the statistical-significance filter:

True Effect Size

Figure from https://rpsychologist.com/cohend/

Observed Effect Size when p < .05.
(hat-tip to the R Psychologist for the figures; https://rpsychologist.com/cohend/)

That’s a big distortion, and it really matters. It means:

  • What seems like a major/breakthrough effect may actually be more modest

  • Follow-up studies done at the same sample-size are more likely than not to fail!

This is the difficult truth about inadequate sample-sizes: it’s not just about the waste of not detecting true effects. Inadequate samples are problematic because the significant findings they generate are likely to be distorted and misleading. It’s very difficult to do fruitful, generative science if what you publish is a distorted view of reality.

References

Anscombe, F. J. 1954. “Fixed-Sample-Size Analysis of Sequential Observations.” Biometrics 10 (1): 89–100. https://doi.org/10.2307/3001665.
Mole. 2017. “Peerless i.” Journal of Cell Science 130: 2079–80. https://doi.org/10.1242/jcs.206375.
———. 2018. “Mea Culpa , Mea Powerful Culpa.” Journal of Cell Biology 131: 215707. https://doi.org/10.1242/jcs.215707.
Simmons, Joseph P., Leif D. Nelson, and Uri Simonsohn. 2011. “False-Positive Psychology: Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant.” Psychological Science 22 (11): 1359–66. https://doi.org/10.1177/0956797611417632.